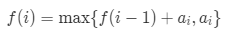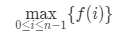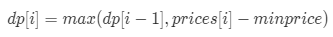题记
刷一下动态规划的简单题,一共也没几道。顺便把前100道题里面的中等难度的动态规划题刷了。
第53、121、198是简单题。
题目
53 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
题解
定义状态转移方程
f(i)表示以i结尾的子串连续子数组的最大和,最后的答案应当是
一开始的想法是定义f(i)是数组前i个数中连续子数组的的最大和,但是发现写不出来转移方程。
代码
1
2
3
4
5
6
7
8
9
|
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
a = nums[0]
result = nums[0]
for i in range(1, len(nums)):
a = max(a+nums[i], nums[i])
result = max(result, a)
return result
|
121 买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
题解
状态转移方程,可以看到前i天:
代码
1
2
3
4
5
6
7
8
9
10
11
|
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) <= 1:
return 0
a = 0
min_price = prices[0]
for i in range(1, len(prices)):
a = max(a, prices[i] - min_price)
if prices[i] < min_price:
min_price = prices[i]
return a
|
198 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
题解
dp 方程为:dp[i] = max(dp[i-2]+nums[i], dp[i-1])
一开始想的很复杂,分享一下心路历程:
dp[i] 分3种情况 1. i-1偷了,i只能不偷,那么dp[i]=dp[i-1],并且要维护一个变量说明i没有偷; 2. i-1没偷,那么可以选择偷i,则有dp[i]=dp[i-1]+nums[i],维护一个状态说明偷了i;3. i-1没偷, i仍然选择不偷,则有dp[i] = dp[i-1],维护一个状态表示i没偷。
这是一开始的分析,显然很复杂,而且如果i-1没偷,那么就一定要偷i才能利益最大化,之所以考虑不偷,是为了让i+1能够偷。真正的思路就是2种情况:1. 偷前k-2个房子,并且偷最后一间 2. 偷前k-1个房子,不偷最后一间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
elif len(nums) == 1:
return nums[0]
a,b = nums[0], max(nums[0],nums[1])
for i in range(2, len(nums)):
tmp = b
b = max(a+nums[i], b)
a = tmp
return b
|
62 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
题解
dp方程为:dp[i][j] = dp[i-1][j] + dp[i][j-1] , 表示走到第i,j个格子有多少种走法,分别是从上面一格和从左边一格走过来。
代码
1
2
3
4
5
6
7
|
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1] * n] + [[1]+[0]*(n-1) for _ in range(m-1)]
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i][j-1] + dp[i-1][j]
return dp[-1][-1]
|
上面的代码空间复杂度是O(m*n),可以进行优化成空间复杂度为O(n)的下面的代码。
1
2
3
4
5
6
7
|
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [1]*n
for i in range(1, m):
for j in range(1, n):
dp[j] = dp[j-1] + dp[j]
return dp[-1]
|
另外这道题还有数学解法,即计算$C_{m+n-2}^{m-1}$.
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [[0] * n for _ in range(m)]
for i in range(m):
if obstacleGrid[i][0] == 0:
dp[i][0] = 1
else:
break
for i in range(n):
print(dp)
if obstacleGrid[0][i] == 0:
dp[0][i] = 1
else:
break
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
continue
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
|
优化空间复杂度O(n+1):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [0] * (n+1)
dp[1] = 1
for i in range(m):
for j in range(n):
print(dp)
if obstacleGrid[i][j] == 1:
dp[j+1] = 0
else:
dp[j+1] = dp[j+1] + dp[j]
return dp[-1]
|
可视化如下表所示,其中表头[0,1,0,0]表示dp初始化的值,括号中的0表示虽然dp没有存第一列但是因为第一列都是0,所以dp[0]一个值就相当于第一列的m个值。
| 0 |
1 |
0 |
0 |
| (0) |
0 |
0 |
0 |
| (0) |
1 |
1 |
0 |
| (0) |
0 |
0 |
0 |
64 最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 输出最小的路径和。
代码
1
2
3
4
5
6
7
8
9
10
|
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m ,n = len(grid), len(grid[0])
dp = [float('inf')]*(n+1)
dp[1] = 0
for i in range(m):
for j in range(n):
dp[j+1] = min(dp[j+1], dp[j]) + grid[i][j]
# print(dp)
return dp[-1]
|
空间复杂度是O(n+1),与62 不同路径的优化方法类似,但是会巧妙地使用inf,使得第一列总是选择上面一格,第一行总是选择左边一格。
比如当输入是[[1,3,1],[1,5,1],[4,2,1]],会进行下表所示的初始化,其中可以发现第一个inf可以模拟成一列inf:
| inf |
0 |
inf |
inf |
| (inf) |
1 |
3 |
1 |
| (inf) |
1 |
5 |
1 |
| (inf) |
4 |
2 |
1 |
另一种方法存dp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m ,n = len(grid), len(grid[0])
for i in range(m):
for j in range(n):
if i==0 and j==0:
continue
if i == 0:
grid[i][j] = grid[i][j-1]+grid[i][j]
elif j == 0:
grid[i][j] = grid[i-1][j]+grid[i][j]
else:
grid[i][j] = min(grid[i-1][j], grid[i][j-1]) + grid[i][j]
return grid[-1][-1]
|
空间复杂度是O(1),因为是直接修改的原矩阵。
91 解码方法

题解
难点是对0的处理,共有4种情况,刚开始只想到了第三个状态方程:
- s[i]是0,后2位<=26,则dp[i]=dp[i-2]。e.g. 110
- s[i]是0,后2位>26,或等于0,则return 0。e.g. 100,190
- s[i]不是0,后两位大于10,或小于等于26,则dp[i]=dp[i-1]+dp[i-2]。e.g. 123,111
- s[i]不是0,后两位小于10(因为末尾不为0,所以没有等于10),或大于26,则dp[i]=dp[i-1]。e.g. 109,199
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution:
def numDecodings(self, s: str) -> int:
if s[0] == '0':
return 0
if len(s) == 1:
return 1
if s[1] == '0':
if int(s[:2]) <= 26:
a,b = 1,1
else:
return 0
else:
if int(s[:2]) <= 26: #由于前面判定过s[0]=='0'了,所以没有大于10的判断
a,b = 1,2
else:
a,b = 1,1
for i in range(2, len(s)):
two_ss = int(s[i-1:i+1])
if s[i] == '0':
if two_ss <= 26 and two_ss != 0:
tmp = b
b = a
a = tmp
else:
return 0
else:
if two_ss > 10 and two_ss <= 26:
tmp = b
b = a + b
a = tmp
else:
# b = b
a = b
return b
|
95 不同的二叉搜索树II
二叉搜索树(Binary Search Tree)的定义:
其左子树(left subtree)下的每个后代节点(descendant node)的值都小于节点 n 的值;
其右子树(right subtree)下的每个后代节点的值都大于节点 n 的值。
一句话概括:左小右大

题解
对于[1,2,3,4]而言:
对1当根节点,则有dp[0], 1, dp[3],左子树为null,右子树为[2,3,4]
对2当根节点,则有dp[1], 2, dp[2],左子树为[1],右子树为[3,4]
对3当根节点,则有dp[2], 3, dp[1],左子树为[1,2],右子树为[4]
对4当根节点,则有dp[3], 4, dp[0],左子树为[1,2,3],右子树为null
代码
递归代码,递归的出口是start>end时,返回None。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
def generateTrees(start, end):
if start > end:
return [None, ]
allTrees = []
for i in range(start, end+1): # 枚举可行根节点
# 获得所有可行的左子树集合
leftTrees = generateTrees(start, i-1)
# 获得所有可行的右子树集合
rightTrees = generateTrees(i+1, end)
# 从左子树集合中选出一棵左子树,从右子树集合中选出一棵右子树,拼接到根节点上
for l in leftTrees:
for r in rightTrees:
currTree = TreeNode(i)
currTree.left = l
currTree.right = r
allTrees.append(currTree)
return allTrees
return generateTrees(1, n) if n else []
|
96 不同的二叉搜索树
给定一个整数 n,求以 1 … n 为节点组成的二叉搜索树有多少种?
题解
可组成的数量就是左子树可组成的数量乘以右子树可组成的数量。
比如[1,2,3,4]:
对1当根节点,则有dp[0]*dp[3],左子树为null,右子树为[2,3,4]
对2当根节点,则有dp[1]*dp[2],左子树为[1],右子树为[3,4]
对3当根节点,则有dp[2]*dp[1],左子树为[1,2],右子树为[4]
对4当根节点,则有dp[3]*dp[0],左子树为[1,2,3],右子树为null
即$dp[n] = \sum_{i=0}^{n-1}dp[i]*dp[n-i-1]$
p.s. 实际上这道题有时间复杂度O(n)和空间复杂度O(1)的卡塔兰数的解法,因为卡塔兰数就是dp[0]=1,dp[1]=1且满足上面递归式的数列。但是先专注于动态规划,卡塔兰数留着以后总结。
代码
代码用递归解法,加上一个表格self.n2result来存储计算过的值,从而减少计算量。(不用表,直接递归会超时)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution:
def __init__(self):
self.n2result = {}
def numTrees(self, n: int) -> int:
if n<=1:
return 1
if n in self.n2result:
return self.n2result[n]
total = 0
for i in range(n):
total += self.numTrees(i) * self.numTrees(n-i-1)
self.n2result[n] = total
return total
|
递归可以换成迭代,自底向上,dp[3]的计算需要dp[0]、dp[1]、dp[2],计算出dp[3]之后就存起来,然后再通过dp[0]…dp[3]计算出dp[4]:
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution:
def numTrees(self, n: int) -> int:
store = [1, 1] # dp[0],dp[1]
if n <= 1:
return store[n]
for m in range(2, n+1):
s = m-1
count = 0
for i in range(m):
count += store[i]*store[s-i]
store.append(count)
return store[n]
|
两种方法时间复杂度都是O($n^2$),空间复杂度是O(n)。