题记

卡特兰数（Catalan number）是组合数学中一个常出现在各种计数问题中的数列。

卡塔兰数算是leetcode里面的高频题目了，这里就来解决一下卡塔兰数问题。

卡塔兰数

卡塔兰数的一般式是：

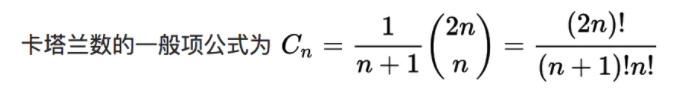
卡塔兰数的等价式为：

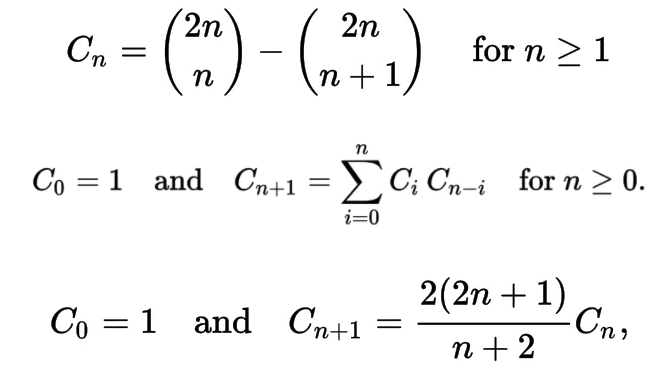
卡塔兰数的题目

96 不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

这道题的动态规划解法我已经在这篇博客里面介绍过了。

解题思路

可组成的数量就是左子树可组成的数量乘以右子树可组成的数量。

比如[1,2,3,4]：

对1当根节点，则有dp[0]*dp[3]，左子树为null，右子树为[2,3,4]

对2当根节点，则有dp[1]*dp[2]，左子树为[1]，右子树为[3,4]

对3当根节点，则有dp[2]*dp[1]，左子树为[1,2]，右子树为[4]

对4当根节点，则有dp[3]*dp[0]，左子树为[1,2,3]，右子树为null

即$dp[n] = \sum_{i=0}^{n-1}dp[i]*dp[n-i-1]$

上式满足卡塔兰数的第二个等价式，可以替换成第三个等价式，从而得到空间复杂度O(1)，时间复杂度O(n)的代码。

代码

1
2
3
4
5
6

class Solution(object):
    def numTrees(self, n):
        C = 1
        for i in range(0, n):
            C = C * 2*(2*i+1)/(i+2)
        return int(C)

同样可以写出卡塔兰数一般式$\frac{1}{n+1}C_{2 n}^{n}$的代码，不过力扣提交结果的执行耗时上上面的代码更好；而acwing 130由于测试用例的n值很大，只有下面使用math库的代码通过了，其他2个都超时了。

使用math库：

1
2
3
4
5
6

import math
class Solution:
    def numTrees(self, n):
        A = math.factorial(2*n)
        B = math.factorial(n)
        return A//B//B//(n+1)

不使用math库（这个代码是三个里面最不推荐的）：

1
2
3
4
5
6
7
8
9

class Solution:
    def numTrees(self, n):
        C = 1
        # print(A//B)
        for i in range(n+1,2*n+1):
            C*=i
        for i in range(1,n+1):
            C=C//i # 这里一定要是整除，不然有精度问题
        return C//(n+1)

进出栈序列

n 个元素进栈序列为：1，2，3，4，...，n，则有多少种出栈序列。

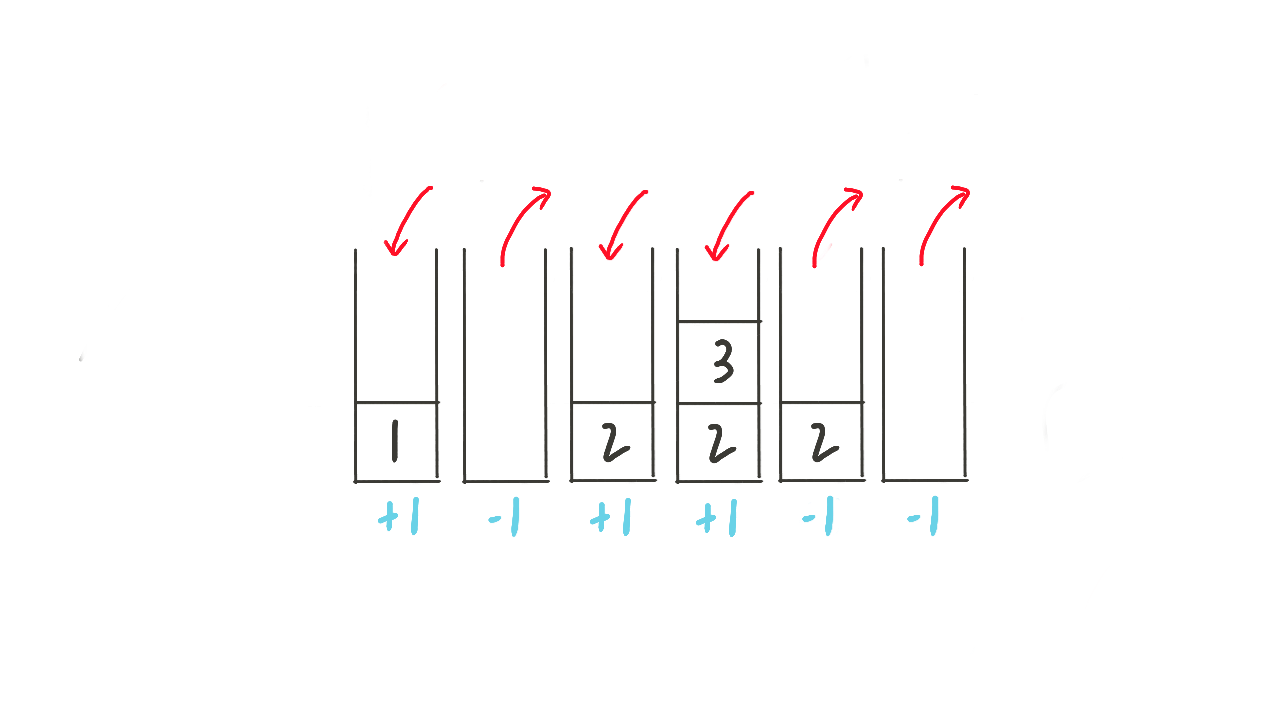
上图所示是一种出栈序列，可以用[+1, -1, +1, +1, -1, -1]来表示 。

所有的-1,+1的排列组合有$C_{2n}^n$个，因为相当于有2n个位置，放n个+1（剩下的位置都是-1）。

但是因为-1之前一定要有足够的+1，如[+1, -1, -1, +1]是不合法的，所以要减去不合法的数量。

观察不合法的序列[+1, -1, -1, +1]，不合法的位置是第3个-1，将前3项取反，得到[-1, +1, +1, +1]。取反后是1个-1和3个+1。

不合法序列总是出现在第2m+1(1、3、5….)处有一个-1，且前2m个数值为m个+1 和 m个-1，后2n-(2m+1)个数里面有n-m个+1 和 n-m-1个-1。

将前2m+1个数取反： 前2m个数字中有m个+1 和 m个-1，第2m+1个数是+1，后2n-(2m+1)个数字中有n-m个+1 和 n-m-1个-1，

n+1个+1 和 n-1个-1的序列共有$C_{2n}^{n+1}$种。

不合法的序列和n+1个+1、n-1个-1序列是一一对应的关系，所以不合法序列的数量为$C_{2n}^{n+1}$。

n=4的不合法序列有：

m=1

[-1, -1, +1, +1] -> [+1, -1, +1, +1]

[-1, +1, -1, +1] -> [+1, +1, -1, +1]

[-1, +1, +1, -1] -> [+1, +1, +1, -1]

m=3

[+1, -1, -1, +1] -> [-1, +1, +1, +1]

最终结果为$C_{2n}^n - C_{2n}^{n+1}$，也就是第一个等价式。

非降路径（另一种解释方法）

画一个nxn的格子，从左下角出发，+1表示向右走一格，-1表示向上走一个，走到右上角为有一个序列。

而不合法的序列就是会走到超过对角线虚线的序列。

下图为n=4的可行走法：

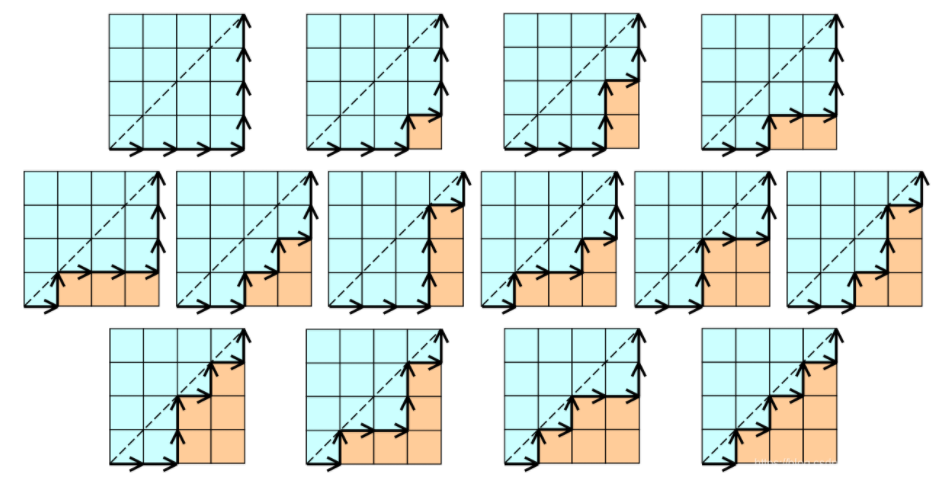
可以发现从左下角走到右上角的步数是一定的，即向右走n步、并向上走n步。转化成排列组合，一共2n步，有n个向右走，剩下的都是向上走，一共有$C_{2n}^n$种走法。

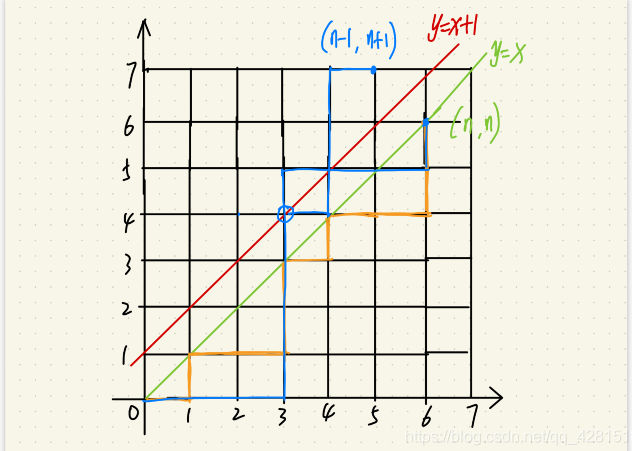
而非法路径的特点是，一定会走到y>=x+1的地方。

如下图所示，到绿色的点(n,n)的蓝线是一条非法路径，其与y=x+1的交点用蓝圈标出，将其后半段作y=x+1的对称，此时得到一条从左下角到蓝色的点(n-1,n+1)的路径。

每一条非法路径作对称操作，都能得到这样的一条路径，到点(n-1, n+1)的路径一共有$C_{2n}^{n+1}$个。

p.s. $C_{2n}^{n+1}$是怎么得到的：一共2n(n-1 + n+1)步，有n+1个向上走，剩下的都是向右走。

括号序列

n 对括号，则有多少种 “括号匹配” 的括号序列

这题和进出栈序列完全一致，左括号是+1，右括号是-1。

相同的问题还有火车进出栈问题（这是acwing的第130题一列火车n节车厢，依次编号为1,2,3,…,n。每节车厢有两种运动方式，进栈与出栈，问n节车厢出栈的可能排列方式有多少种。acwing的测试样例的n值很大，有个测试用例n是15000，结果手写的阶乘超时了，手写阶乘运算会有精度问题，python用个math库可以解决精度问题，C的话要用质因数分解解决精度问题）

买票找零

《编程之美》4.3买票找零：2n个人排队买票，其中n个人持50元，n个人持100元。每张票50元，且一人只买一张票。初始时售票处没有零钱找零。请问这2n个人一共有多少种排队顺序，不至于使售票处找不开钱？

50相当于进栈、100相当于出栈。

证明

递推式推通项式：https://zhuanlan.zhihu.com/p/56821103 感觉这个证明还是挺难的。

除递推式以外的证明：链接 这个相对来说就简单多了

参考资料

• 「算法入门笔记」卡特兰数 https://leetcode-cn.com/circle/article/lWYCzv/

• AcWing 130. 火车进出栈问题（卡特兰数、高精度、分解质因数） https://blog.csdn.net/qq_42815188/article/details/104286409?utm_medium=distribute.pc_relevant.none-task-blog-title-2&spm=1001.2101.3001.4242