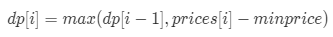题记
leetcode上刷动态规划有几道股票题,索性就一起刷了。
题目
121 买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
只是一道动态规划的简单题,在之前的博客里总结过了。
状态转移方程,可以看到前i天:
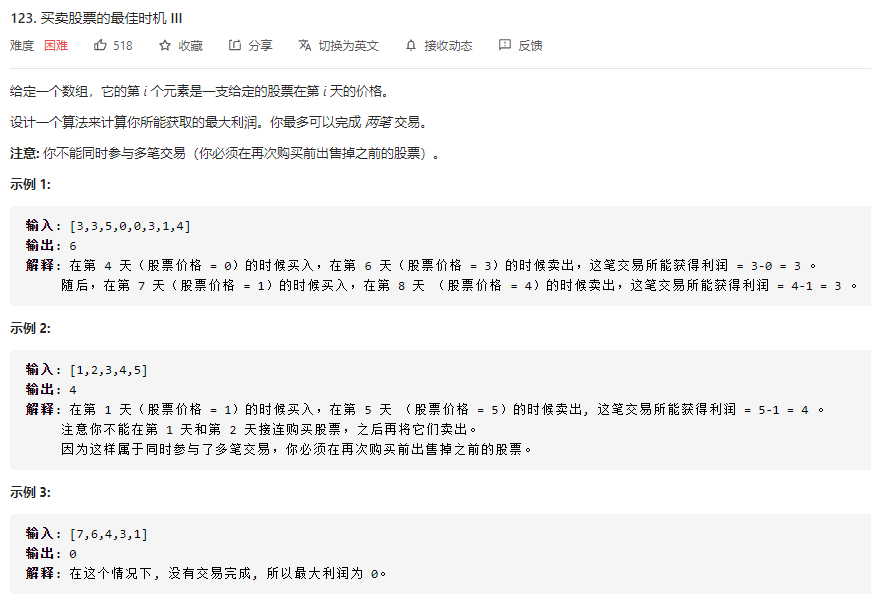
123 买卖股票的最佳时机 III

与121的区别在于最多可以完成2次交易,就让简单题变成了困难题。
最开始的思路就是遇到降了就卖,最后做一个排序,比如131419,获得收益是2、3、8,排完序之后求最大的两个3、8之和,但是这样解决不了132719,因为这样得到是2、5、8,排序相加结果是13,但是实际上1买7卖收益最大,结果是6+8=14。
没想通,直接看题解了。
定义二维数组 dp[n][4]这的n表示天数,4表示4种不同的状态:
dp1[i][0]:第一次买入;
dp2[i][1]:第一次卖出;
dp3[i][2]:第二次买入;
dp4[i][3]:第二次卖出。
第一次买卖:
第一次买入:第一次买入后保持不动, 或者从初始状态转换而来
dp[i][0] = max(dp[i-1][0], -prices[i])
第一次卖出:第一次卖出后保持不动,或者从第一次买入转换而来
dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i])
第二次买卖:
第二次买入:第二次买入后保持不动, 或者从第一次卖出转换而来
dp[i][2] = max(dp[i-1][2], dp[i][1] -prices[i])
第二次卖出:第二次卖出后保持不动,或者从第二次买入转换而来
dp[i][3] = max(dp[i-1][3], dp[i-1][2]+prices[i])
132719的状态如下表所示,不加粗表示保持不动,加粗表示对当前天进行了买卖操作。
|
day1 |
day2 |
day3 |
day4 |
day5 |
day6 |
|
1 |
3 |
2 |
7 |
1 |
9 |
| 第一次买 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
| 第一次卖 |
0 |
2 |
2 |
6 |
6 |
8 |
| 第二次买 |
-1 |
-1 |
0 |
0 |
5 |
5 |
| 第二次卖 |
0 |
2 |
2 |
2 |
2 |
14 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) <= 1:
return 0
days = len(prices)
dp = [[0] * 4 for _ in range(days)]
dp[0][0] = -prices[0] # 第一天第一次买入
dp[0][2] = -prices[0] # 第一天第二次买入
for i in range(1, days):
# 第一次买入卖出
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
# 第二次买入卖出
dp[i][2] = max(dp[i-1][2], dp[i-1][1] - prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2] + prices[i])
return max(0, dp[-1][0], dp[-1][3])
|
由于第i天只依赖于第i-1天,所以可以优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) <= 1:
return 0
days = len(prices)
dp1 = 0
dp3 = 0
dp0 = -prices[0] # 第一天第一次买入
dp2 = -prices[0] # 第一天第二次买入
for i in range(1, days):
# 第一次买入卖出
dp0 = max(dp0, -prices[i])
dp1 = max(dp1, dp0 + prices[i]) # 实际上这一行放在上上行更好理解
# 第二次买入卖出
dp2 = max(dp2, dp1 - prices[i])
dp3 = max(dp3, dp2 + prices[i])
return max(dp1, dp3)
|
188. 买卖股票的最佳时机 IV
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
和123题思路完全一样,但是要加上一个对k值的判别,否则提交之后会报内存错误。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if len(prices) <= 1 or k<=0:
return 0
days = len(prices)
# 当k非常大时转为无限次交易,否则会造成Memory Error
if k > days//2:
dp0, dp1 = 0, -prices[0]
for i in range(1, days):
dp0 = max(dp0, dp1+prices[i])
dp1 = max(dp1, dp0-prices[i])
return max(dp0, dp1)
dp = [0] * k*2
for i in range(k*2):
if i%2 == 0:
dp[i] = - prices[0]
for i in range(1, days):
dp[1] = max(dp[1], dp[0] + prices[i])
dp[0] = max(dp[0], 0 - prices[i])
# dp[3] = max(dp[3], dp[2] + prices[i])
# dp[2] = max(dp[2], dp[1] - prices[i])
#
# dp[4] = max(dp[4], dp[3]+prices[i])
# dp[3] = max(dp[3], dp[2]-prices[i])
for j in range(k-1):
dp[2*j+3] = max(dp[2*j+3], dp[2*j+2] + prices[i])
dp[2*j+2] = max(dp[2*j+2], dp[2*j+1] - prices[i])
# print(dp)
return max(dp)
|