Leetcode数组和字符串

草祭收录于算法

2020-11-02 约 4128 字预计阅读 9 分钟

题记

看到一个说法，面试考数组、字符串题的频率最高，所以来刷一下这类题。这次根据leetocde提供的教程的顺序来学习。

数组简介

寻找数组的中心索引

定义数组 中心索引 的：数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和，若没有中心索引返回-1。

输入：nums = [1, 7, 3, 6, 5, 6]

输出：3

解释：索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11)，与右侧数之和 (5 + 6 = 11) 相等。同时, 3 也是第一个符合要求的中心索引。

1
2
3
4
5
6
7
8
9


class Solution(object):
    def pivotIndex(self, nums):
        S = sum(nums)
        leftsum = 0
        for i, x in enumerate(nums):
            if leftsum == (S - leftsum - x):
                return i
            leftsum += x
        return -1

要点是找到左右节点之和的关系：leftsum==S-nums[i]-leftsum

搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

输入: [1,3,5,6], 5

输出: 2

一开始用一个for循环顺序遍历实现了O(n)的代码，但是这种排序数组寻找目标值首先应该想到O(logN)的二分法。

二分法找第一个

1
2
3
4
5
6
7
8


def lower_bound(array, first, last, value):
	while first < last: # 搜索区间[first, last)不为空
        mid = first + (last - first)//2 # 防溢出
        if array[mid] < value:
            first = mid + 1
        else:
            last = mid
    return first # last也行，因为此时重合

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        first, last =0, len(nums)
        while first < last: # 搜索区间[first, last)不为空
            mid = first + (last - first)//2 # 防溢出
            if nums[mid] < target:
                first = mid + 1
            else:
                last = mid
        return first # last也行，因为此时重合

二维数组

旋转矩阵

给你一幅由 N × N 矩阵表示的图像，其中每个像素的大小为 4 字节。请你设计一种算法，将图像旋转 90 度。

不占用额外内存空间能否做到？

一道中等难度题，tag里面只有数组，我觉得应该加上数学的tag，顺带一提这是剑指offer里的题，微软面试也出过。

旋转矩阵就是先上下翻转，再对角线翻转。

1 2 3 | 7 8 9 | 7 4 1

4 5 6 | 4 5 6 | 8 5 2

7 8 9 | 1 2 3 | 9 6 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # 水平翻转
        for i in range(n // 2):
            for j in range(n):
                matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
        # 主对角线翻转
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

零矩阵

编写一种算法，若M × N矩阵中某个元素为0，则将其所在的行与列清零。

一道非常简单的题，一开始用两个set记录实现了，不过教科书式的写法是灵活使用原矩阵的第一行和第一列，即用第一行和第一列代替2个set，并用2个变量记录第一行和第一列的状态。

代码就略了，因为很简单，就是用第一行、第一列记录的思路不容易马上想。

对角线遍历

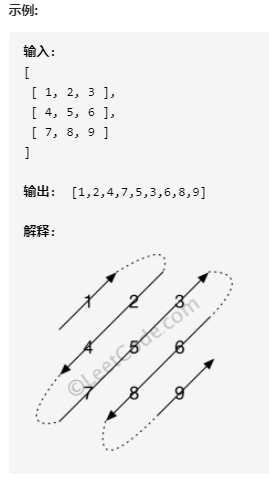
给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

可以分成2种情况：从左下到右上、从右上到左下，总共遍历m+n-1次。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution:
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix:
            return []
        m,n = len(matrix), len(matrix[0])
        res = []
        for ii in range(m+n-1):
            if ii%2 == 0:
                # 从左下向右上
                if ii < m:
                    # 开始点为最左边(ii,0)
                    i, j = ii, 0
                else:
                    # 开始点为最下行
                    i, j = m - 1, ii - m + 1
                while i >= 0 and j < n:
                    res.append(matrix[i][j])
                    i -= 1
                    j += 1
            else:
                # 从右上到左下
                if ii < n:
                    i, j = 0, ii
                else:
                    i, j = ii - n + 1, n - 1
                while i < m and j >= 0:
                    res.append(matrix[i][j])
                    i += 1
                    j -= 1
        return res

字符串简介

最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad” 输出: “bab” 注意: “aba” 也是一个有效答案。

示例 2：

输入: “cbbd” 输出: “bb”

这题很早就见过，不过一直放着了，其实也挺简单的，下面是别人的题解。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution:
    def longestPalindrome(self, s: str) -> str:
        size = len(s)
        if size < 2:
            return s
        # 至少是 1
        max_len = 1
        res = s[0]

        for i in range(size):
            palindrome_odd, odd_len = self.__center_spread(s, size, i, i)
            palindrome_even, even_len = self.__center_spread(s, size, i, i + 1)

            # 当前找到的最长回文子串
            cur_max_sub = palindrome_odd if odd_len >= even_len else palindrome_even
            if len(cur_max_sub) > max_len:
                max_len = len(cur_max_sub)
                res = cur_max_sub

        return res

    def __center_spread(self, s, size, left, right):
        """
        left = right 的时候，此时回文中心是一个字符，回文串的长度是奇数
        right = left + 1 的时候，此时回文中心是一个空隙，回文串的长度是偶数
        """
        i = left
        j = right

        while i >= 0 and j < size and s[i] == s[j]:
            i -= 1
            j += 1
        return s[i + 1:j], j - i - 1

（选修）字符串匹配算法：KMP

Knuth–Morris–Pratt（KMP）算法是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。它的时间复杂度是 O(m+n)。KMP看文字贼难搞，看动画就很容易学了，视频教程。

28. 实现 strStr()

这道题被归到简单题，大概因为暴力法真的很容易想到，复杂度是O(m*n)。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        for i in range(len(haystack)-len(needle)+1):
            match = True
            for j in range(len(needle)):
                if needle[j] != haystack[i+j]:
                    match = False
                    break
            if match:
                return i

        return -1

不过有时候好像会问用KMP解这道题，貌似一般不要求手撕，但是需要知道KMP算法的思路。

通过视频教程转化成代码深入理解一下：

如下图示，找最长公共前后缀，比如ABBAB的最长公共前后缀是AB。

如下图示（这里下标从1开始），定义主串的当前位置是出现不匹配的位置：

模式串（黄色数组）一号位不匹配时，下一次比较是模式串1号位与主串的下一位比较。

模式串二号位不匹配时，下一次比较是模式串1号位（A没有最长公共前后缀）与主串的当前位比较。

模式串三号位不匹配时，下一次比较是模式串1号位（AB没有最长公共前后缀）与主串的当前位比较。

模式串四号位不匹配时，下一次比较是模式串2号位（ABA最长公共前后缀是A）与主串的当前位比较。

模式串五号位不匹配时，下一次比较是模式串3号位（ABAB最长公共前后缀是AB）与主串的当前位比较。

模式串六号位不匹配时，下一次比较是模式串4号位（ABABA最长公共前后缀是ABA）与主串的当前位比较。（即下图所示）

模式串n号位不匹配时，下一次比较是模式串前n-1数组的最长公共前后缀中，公共前缀结束的后一位（等于最大公共前后缀长度+1）与主串的当前位比较。

我自己再举个例子：主串： ABABABC

模式串：ABABC

第一次匹配匹配到主串当前位置A的时候，出现不匹配：

A	B	A	B	A	B	C
A	B	A	B	C

移动模式串，公共前后缀一定匹配(红色)所以无需再比，直接从主串当前位置和5号位(与视频保持一致，从1开始索引)的next位置（蓝色的A）开始对比：

A	B	A	B	A	B	C
		A	B	A	B	C

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


int match (char* P, char* S){ // KMP 算法
    int* next = buildNext(P); // 构造 next 表
    int m = (int) strlen (S), i = 0; // 文本串指针
    int n = (int) strlen(P), j = 0; //模式串指针
    while (j < n && i < m) // 自左向右逐个比对字符
        if (0 > j || S[i] == P[j]) // 若匹配，或 P 已移除最左侧
            {i++; j++;} // 则转到下一字符
        else
            j = next[j]; // 模式串右移（注意：文本串不用回退）
    delete [] next; // 释放 next 表
    return i - j;
}

int* buildNext(char* P) { // 构造模式串 P 的 next 表
    size_t m = strlen(P), j = 0; // “主”串指针
    int* N = new int[m]; // next 表
    int  t = N[0] = -1; // 模式串指针
    while (j < m - 1)
        if ( 0 > t || P[j] == P[t]){ // 匹配
            j++; t++;
            N[j] = t; // 此句可改进为 N[j] = (P[j] != P[t] ? t : N[t]);
        }else // 失配
        t = N[t];
    return N;

}

双指针技巧

1. 两个指针分别指向数组的开头及末尾

两数之和 II - 输入有序数组

两数之和很容易想到$O(n^2)$的暴力法，还有利用哈希表的空间和时间复杂度O(n)的方法，但是如果输入有序，可以用双指针实现空间复杂度O(1)，时间复杂度O(n)的方法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        i, j = 0, len(numbers) - 1
        while i<j:
            if numbers[i] + numbers[j] == target:
                return [i+1, j+1]
            elif numbers[i] + numbers[j] < target:
                i+=1
            else:
                j-=1
        return [-1, -1]

双指针，如果和小，左指针移动；如果和大，右指针移动。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        low, high = 0, len(numbers) - 1
        while low < high:
            total = numbers[low] + numbers[high]
            if total == target:
                return [low + 1, high + 1]
            elif total < target:
                low += 1
            else:
                high -= 1

        return [-1, -1]

2. 快慢指针

移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。元素的顺序可以改变。

一开始很快就用pop函数实现了，但是发现好像复杂度是$O(n^2)$，极端情况是所有元素都pop一遍，但是pop一次的时间复杂度是O(n)，感觉还是少用pop解题的好，虽然很好想到，而且其实在leetcode里面这个方法用python比双指针击败的要多。

一开始想到的方法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        i = 0
        cur_len = len(nums)
        while i < cur_len:
            if nums[i]!=val:
                i+=1
            else:
                nums.pop(i)
                cur_len-=1

        return cur_len

快慢指针，如果快指针指向的不是移除元素，快慢指针都向前进；如果快指针指向需要移除的元素，快指针先走一步，当快指针走到不需要移除的元素的时候，复制快指针指向的值给慢指针，会覆盖掉需要移除的元素。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        a = 0
        b = 0

        while a < len(nums):
            if nums[a] != val:
                nums[b] = nums[a]
                b += 1
            a += 1

        return b

再优化，这里题目有一句不要求顺序一致，实际上上面实现的还是顺序一致的，当出现num=[4，1，2，3，5] val=4时，1，2，3，5会向左复制一遍，实际上不需要，可以换一次，即[5, 1，2，3，4]，然后数组长度减一，就不会再遍历到最后一个4了，但是也有可能交换到的还是4（即5的位置是4的情况），这时候再判断一次就可以了。

时间复杂度是O(n)，交换位置的次数等于要删除元素的个数，所以如果要删除的元素数量少的话，效率就高。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        cur_len = len(nums)
        i = 0
        while i < cur_len:
            if nums[i] == val:
                nums[i], nums[cur_len-1] = nums[cur_len - 1], nums[i]
                cur_len -= 1
            else:
                i+=1
        return cur_len

最大连续1的个数

给定一个二进制数组，计算其中最大连续1的个数。

示例 1: 输入: [1,1,0,1,1,1] 输出: 3

解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.

非常简单的实现了：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        res = 0
        count = 0
        for i in range(len(nums)):
            if nums[i] == 1:
                count += 1
                res = max(res, count)
            else:
                count = 0
        return res

万一面试要求双指针的题解，两个指针分别指向1的最前面和最后面，这里用一个小的技巧就是末尾加上一个0：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        i = -1
        res = 0
        nums+=[0]
        for j in range(len(nums)):
            if nums[j] == 1:
                continue
            else:
                res = max(res, j - i - 1)
                i = j
        # 如果末尾不加零需要额外的判断        
        # if nums[j] == 1:
        #    res = max(res, j - i)
        return res
    

长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：输入：s = 7, nums = [2,3,1,2,4,3] 输出：2

解释：子数组 [4,3] 是该条件下的长度最小的子数组

一道中等难度的双指针题，画一下图，O(n)复杂度的代码不难想(反而有个O(nlogn)的算法是难想的，这里就不写了)：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        i, j =0, 0
        res = len(nums) + 1
        tmp_sum = 0
        while j < len(nums):
            tmp_sum += nums[j]
            while tmp_sum >= s:
                res = min(j - i + 1, res)
                tmp_sum -= nums[i]
                i += 1
            j += 1
        
        if res == len(nums) + 1:
            return 0
        else:
            return res

目录