Leetcode动态规划几道题

草祭收录于算法

2020-10-06 约 1628 字预计阅读 4 分钟

题记

这一篇是Leetcode动态规划简单题之后的又一个关于动态规划的博客，主要按照leetcode的tag里面写的，可能会不定期更新吧

题目

32 最长有效括号

给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

输入: “(()”

输出: 2

解释: 最长有效括号子串为 “()”

注意. “()(())“有效长度是6。

题解

主要是情况有点多，慢慢想都能解出来。

定义状态dp[i]以第i个括号结尾的符号中有效括号串的长度。

第一个大类别是以’(‘均不能组成有效括号串，所以dp为0.

第二个大类有2种情况(粗体字表示s[i-1])：1. ()() 2. a. ()())) b. ()(())) c. ()((()))

第一种情况是dp[i]=dp[i-2]+2，第二种情况(a和c可以合并成一种情况，不过我就按照我第一次写这道题的思路写了): a. 如果dp[i-1]==0, dp[i]=0

b. 如果dp[i-1]!=0, 前面(指s[i- dp[i-1] -1])有可以组成括号的,则dp[i]=dp[i-1]+2

c. 如果dp[i-1]!=0, 前面没有可以组成括号的,则dp[i]=0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if len(s)<2:
            return 0
        result = 0
        dp = [0] * len(s)
        if s[:2] == '()':
            dp[1] = 2
            result = 2
        for i in range(2, len(s)):
            if s[i] == '(': # 第一个大类别
                continue
            # 第二个大类别 s[i] == ')'
            if s[i-1] == '(':
                dp[i] = dp[i-2] + 2
                result = max(result, dp[i])
            else:
                if dp[i-1] == 0:
                    dp[i] = 0
                else:
                    if i-dp[i-1]-1 >= 0 and s[i-dp[i-1]-1] == '(':
                        dp[i] = dp[i-1] + 2
                        if i-dp[i-1]-2 >= 0: #有个python答案里面不做这个判决，因为边界dp[-1]为0
                            dp[i] += dp[i-dp[i-1]-2]
                        result = max(result, dp[i])
                    else:
                        dp[i] = 0


        return result

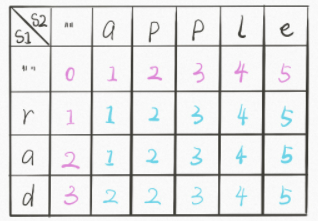
72 编辑距离

p.s. 编辑距离算法被数据科学家广泛应用，是用作机器翻译和语音识别评价标准的基本算法。

题解

这个题第一眼看的毫无头绪，直接看别人的题解了。

参考资料：编辑距离面试题详解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m,n = len(word1), len(word2)
        dp = [[0]*(n+1) for _ in range(m+1)]
        for i in range(m):
            dp[i+1][0] = i+1
        for j in range(n):
            dp[0][j+1] = j+1
        for i in range(m):
            for j in range(n):
                if word1[i] == word2[j]:
                    dp[i+1][j+1] = dp[i][j]
                else:
                    dp[i+1][j+1] = min(dp[i+1][j], dp[i][j+1], dp[i][j]) + 1

        return dp[m][n]

85 最大矩形

120 三角形最小路径和

题解

我最开始想到的状态转移方程：dp[i][j] = tri[i][j] + min( dp[i-1][j] , dp[i-1][j] )，不过这个是从下往上找到最小路径和，所以结果是tri[m-1][0] ，tri[i][j]实际上是tri[-i-1][j]。

1 dp[2][0] triangle[-3][0]
2 dp[1][0] triangle[-2][0]	3 dp[1][1] triangle[-2][1]
4 dp[0][0] triangle[-1][0]	5 dp[0][1] triangle[-1][1]	6 dp[0][2] triangle[-1][2]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        m,n = len(triangle), len(triangle[-1]) # m行n列
        dp = [[0]*n for _ in range(m)]
        for i in range(n):
            dp[0][i] = triangle[-1][i]
        for i in range(1,m):
            for j in range(len(triangle[-i-1])):
                dp[i][j] = triangle[-i-1][j] + min(dp[i-1][j], dp[i-1][j+1])
        return dp[m-1][0]

上面代码的空间复杂度是O(m*n)，由于dp只依赖于相邻行，所以很容易优化成O(n)，n是底层列数。(实际上行数和列数相等，即m=n，所以也可以说O(m))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        n = len(triangle)
        dp =[0]*n
        for i in range(n):
            dp[i] = triangle[-1][i]
        for i in range(1,n):
            for j in range(len(triangle[-i-1])):
                dp[j] = triangle[-i-1][j] + min(dp[j], dp[j+1])
        return dp[0]

139 单词拆分

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

先给我自己的思路，dp[i]表示以第i个字母结尾的子字符串是否能够匹配上。

状态转移方程为：dp[i] = dp[i-匹配的单词长度] && 第i-匹配的单词长度+1 到第i个字母所组成的单词在字典里，这里处理一下边界i-word_size。

例如，假设字典为：is、son、song：

i	s	s	o	n	g	i	s
False	True	False	False	True	True	False	True

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        size = len(s)
        dp = [False] * size
        for i in range(size):
            for word in wordDict:
                word_size = len(word)
                if s[i-word_size+1: i+1] == word and (dp[i-word_size] is True or i-word_size<0):
                    dp[i] = True
        return dp[-1]

152 乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。输入: [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

dp1为前i个子数组所得到的最大非负数乘积，dp2为前i个子数组所得到的最大非正数乘积。

重点是做一个分类讨论，nums[i]为负数和正数的情况。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        res = nums[0]
        dp1 = max(0, nums[0])
        dp2 = min(0, nums[0])
        for i in range(1, len(nums)):
            if nums[i] == 0:
                dp1,dp2 = 0,0
            elif nums[i] > 0:
                dp1 = max(dp1*nums[i], nums[i]) # dp1可能为0，若为0取nums[i]
                dp2 *= nums[i] # 正数乘正数
            else:
                tmp = dp1
                dp1 = dp2 * nums[i]
                dp2 = min(tmp * nums[i], nums[i])
            # print(dp1,dp2)
            res = max(res, dp1)

        return res

目录