音频重采样简述

2020-03-20 约 1925 字预计阅读 4 分钟

题记

需要实现一个音频重采样的功能，发现没有我想象的那么简单，这里通过学习python中librosa的代码，来学习一下重采样，这里将以48kHz下采样到8kHz为例进行讲解。为方便阅读，本文将采样频率写成sr（sampling rate）。注意本文并没有最终实现一个性能很好的重采样程序。

原始48kHz音频：p232_072.wav 点击下载

最简单的实现输出音频：my_p232_072_8kHz.wav 点击下载

librosa重采样输出音频：p232_072_8kHz.wav 点击下载

重采样代码2.0输出音频：my2_p232_072_8kHz.wav 点击下载

最简单的实现

每4(4=48/8)个采样点取一个点.

1
2
3
4
5
6
7
8
9


# 直接每隔times个采样点取一个值
def my_downsample(data,input_sr,output_sr):
    assert input_sr%output_sr == 0
    times = input_sr//output_sr
    out = np.empty(len(data)//times+1)
    for i, d in enumerate(data):
        if i%times == 2:
            out[i//times] = data[i]
    return out

从结果上来看，好像勉强成功了，但是与librosa的实现相比，明显多了很多噪声，为什么会这样呢？

混叠

当采样频率设置不合理时，即采样频率低于2倍的信号频率时，会导致原本的高频信号被采样成低频信号。如下图所示，红色信号是原始的高频信号，但是由于采样频率不满足采样定理的要求，导致实际采样点如图中蓝色实心点所示，将这些蓝色实际采样点连成曲线，可以明显地看出这是一个低频信号。在图示的时间长度内，原始红色信号有18个周期，但采样后的蓝色信号只有2个周期。也就是采样后的信号频率成分为原始信号频率成分的1/9，这就是所谓的混叠：高频混叠成低频了。——参考资料[1]

如上图所示，频率分别为4500Hz和5500Hz的信号，经过相同的sr10000之后，采样结果完全相同。

我們對 5500 Hz 訊號用 10000 的取樣率得到的結果跟 4500 Hz 的結果是分不出來的。同樣 7700 Hz 與 2300 Hz 的結果也是分不出來，9900 Hz 與 100 Hz 也是。這個效應叫做 aliasing，因為高頻訊號被取樣時，他變得跟低頻的一樣。在這個例子，10000 取樣率的一半是 5000，就是我們可取率的最高頻率。超過 5000 的頻率，就會被折掉 5000 Hz。這個取樣率的上限就因此叫做折疊頻率。它有時也被叫做奈奎斯特頻率。請參閱 http://en.wikipedia.org/wiki/Nyquist_frequency 如果 aliasing 頻率被折到低於 0，這折疊頻率要再繼續折。例如，1100 Hz 的三角波的第 5 個諧波是在 12100 Hz，折疊頻率是 5000 Hz，那它應該出現在 -2100 Hz，但它應該對 0 Hz 折一次，就變成出現在 2100 Hz。事實上，在圖2.4 裡你可以看到有個小尖峰在 2100 Hz，再下一個是在 4300 Hz。 ——参考资料[2]

另一个例子: 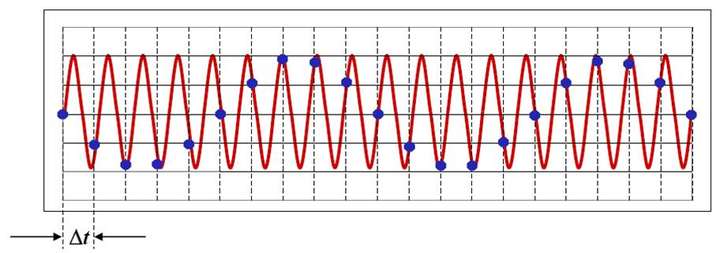上图可以观察得:

红色线所表示的信号在20个Δt的时间里，走过了18个周期（数波峰数量就行了），也就是说它的实际信号频率是$\frac{18}{20Δt}$。

而如果我们每隔一个Δt采样一次，即采样率sr为$\frac{1}{Δt}$。

而蓝色的线就展示了，采样之后原始信号被解释成了频率为$\frac{2}{20Δt}$的信号。

最简单的实现方法里之所以多了很多噪声，是因为将高频(高指的是高于采样率一半)的信号转化成了更低频的信号。那么如果在最简单的实现方法之前加入一个低通滤波器，就可以过滤掉可能会造成混叠的高频信号。

重采样代码2.0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


from scipy import signal
import soundfile as sf

data,sr = sf.read('p232_072.wav')
Fs_highest = 4000
wn=2*Fs_highest/sr #要滤除Fs_highest hz以上频率成分
b, a = signal.butter(8, wn, 'lowpass')   #配置滤波器 8 表示滤波器的阶数 
filtedData = signal.filtfilt(b, a, data)  #data为要过滤的信号
new = my_downsample(filtedData,48000,8000)
sf.write('my2_p232_072_8kHz.wav',new,8000)

效果相比第一种方法有很大提升.

重采样代码3.0

取times个采样点的平均值，而不是每times个点取一次。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 计算times个采样点的平均值作为一个采样点
def my_downsample_avg(data,input_sr,output_sr):
    assert input_sr%output_sr == 0
    times = input_sr//output_sr
    out = np.empty(len(data)//times+1)
    accu = 0
    for i, d in enumerate(data):
        accu+=data[i]
        if i%times == 3:
            out[i//times] = accu/4
            accu = 0
    return out

v3 = my_downsample_avg(data,48000,8000)
sf.write('my3_p232_072_8kHz.wav',v3,8000)

效果比v1要好,但是波形幅度有一些变化.

在前面加一个低通滤波器之后，效果上和v2差距不大，波形的幅值有些变化。

后记

在信号处理上，反转180度称作卷积，直接滑动计算称作自相关，在大部分深度学习框架(包括tensorflow和pytorch)上都没有反转180度的操作。
关于滤波器之类的我也没有深入去了解，所以就略过了。这篇博客只是想说明一下重采样不是那么简单的，以及混叠现象的存在。

参考资料

[1] 什么是混叠? https://zhuanlan.zhihu.com/p/23923059
[2] [超譯]ThinkDSP 第二章 http://timag-shield.blogspot.com/2017/04/thinkdsp_27.html
[3] 几种常见窗函数的特性 https://blog.csdn.net/juhou/article/details/81194566
[4] 在定义卷积时为什么要对其中一个函数进行翻转？ https://www.zhihu.com/question/20500497
[5] 卷积要旋转180度 https://www.jianshu.com/p/8dfe02b61686
[7] Resampling a sound sample, what filter do I use? https://stackoverflow.com/questions/4393545/resampling-a-sound-sample-what-filter-do-i-use
[8] filtfilt源代码 https://github.com/scipy/scipy/blob/v1.4.1/scipy/signal/signaltools.py#L3687-L3885
[9] lfilter源代码https://github.com/scipy/scipy/blob/adc4f4f7bab120ccfab9383aba272954a0a12fb0/scipy/signal/signaltools.py#L1695
[10] Applying filter in scipy.signal: Use lfilter or filtfilt? https://dsp.stackexchange.com/questions/19084/applying-filter-in-scipy-signal-use-lfilter-or-filtfilt
[11] 模拟低通滤波器陈后金 https://www.bilibili.com/video/av26706434/?p=51&t=91
[12] scipy.signal.resample https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.resample.html

目录

音频重采样简述

题记

最简单的实现

混叠

重采样代码2.0

重采样代码3.0

后记

参考资料