题目

题目一. N个人去旅行，在旅店开了N个房间，钥匙挂在大厅的墙上，钥匙上没有标号，每人随手拿一把钥匙，请用程序实现算出所有人都拿错钥匙的可能性有几种。

题目二. N个人坐在六把椅子上，不能坐自己的，有几种坐法。

以上问题可以统称为错排问题。

思考

刚开始以为答案是(n-1)!，这里的思路是第一个人有n-1个可能拿错的钥匙，第二个人有n-2个，以此类推。

实际上并不是，因为有2种情况：

1. 第一个人拿了第二个人的钥匙，那么第二个人此时有n-1个可能拿错的钥匙。第二个人拿错钥匙的可能性有1、3、4、…、N
2. 第一个人拿的不是第二个人的钥匙，那么第二个人此时有n-2个可能拿错的钥匙。假设第一个人拿的是3，那么第二个人拿错钥匙可能性有1、4、…、N

所以并不是(n-1)!，实际上应当是：

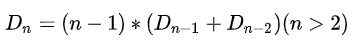
推导

记D(N)为有N个人时的可能性个数。

N=2

D(N) = 1

N=3

D(N) = 2

N=4

D(N) = 9

刚开始推找不到规律就很难，但是发现规律了就简单了。

观察N=4的情况，对第一个人而言，可以拿N-1个人的钥匙，如果第一个人拿的是第k个人的钥匙，此时将问题分为2类问题：

1. 第一个人的钥匙与第k个人的钥匙交换
2. 第一个人的钥匙没有进行交换，即第一个人拿了第k把钥匙，但是第k个人拿的却不是第一把钥匙。

如上表所示，如果进行了交换的，用红字标出，现在讨论表中前3行。

1. 发生交换：当k=2时，此时问题变成第3个人和第4个人，第3把钥匙和第4把钥匙的分配问题，即2个人、2把钥匙的错排问题，有D(2)种情况，可以推广到D(N-2)。
2. 不做交换：当k=2时，此时问题变成了第2、3、4个人，第1，4，3把钥匙的分配问题。实际上，可以将第1把钥匙看作是第2把钥匙，因为第1把钥匙不能给第2个人（因为这种情况就是交换钥匙，包括在D(2)里面了）。如下表所示，问题变成3个人、3把钥匙的错排问题，有D（N-1）种情况：

由于k可以取值N-1个，所以一共是D(N) = (N-1)*( D(N-1) + D(N-2) )

代码的话就跟爬楼梯问题基本是一样的，这里给个参考代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 0
        elif n == 2:
            return 1
        elif n == 3:
            return 2
        a,b = 1,2
        for i in range(4, n+1):
            tmp = b
            b = (i-1) * (b + a)
            a = tmp

        return b