并查集

2019-09-05 约 1423 字预计阅读 3 分钟

题记

今天上了数理统计和数学模型与优化，感觉终于上到了我认为的好课。第一眼看到数学模型与优化的董文永老师感觉自带气场，带着帽子上课，不过讲课还是挺幽默的。非常想吐槽一下教室的设备，两个教室的麦克风完全没声音，幸好坐在前排，要是抢不到位置估计很难听到吧（或者是我带耳机久了，听力下降了吗）。

上数学模型与优化的时候，有道题还是没弄清楚，所以这里来解决一下。这道题的解法不止一种，课上老师介绍的方法是并查集。

NOIP 2015 信息传递

点击展开题目详情

以下的所有说明围绕样例进行说明。

当从别人那里得知自己的生日，实质上就是形成了一个环。所以这道题实际上是：
找到所构建的图中的最小环的长度。

找最小环的过程，这里我们用并查集的方法。即把每个同学都看成点，A同学将信息传给B同学，就相当于在A和B之间建立了一条有向条边，将其加入并查集中，当遇到两个点的祖先节点相同时，则说明他们已经在同一个集合，那么就能构成环，此时判断一下环的长度即可。

Step 0. 初始化

初始化的状态可以表示成下图所示，此时我们把每个节点看成一棵只有一个节点的树，那么每棵树的根自然就是唯一的那个节点。

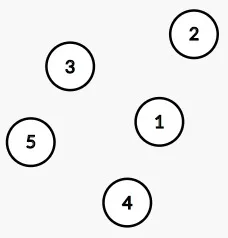
代码来表示上图，创建两个数组a和b，其中a中每个元素表示每棵树的根节点，b来存放传递信息的方向。
为了方便起见，这里的index 0设置为空。

index	1	2	3	4	5
a	1	2	3	4	5
b	2	4	2	3	1

从左到右开始同时扫描一遍两个数组(即一个for循环)。

Step 1. 扫描1

当扫描到1时，发现1传递信息给2(即b[1]值为2)，可以用以下的有向图表示。

此时1和2连在了一起，从两棵树合并成了一棵树，树的根我们定义成所指向的那个节点（需要注意, 并查集是孩子节点指向父节点，这点与一般的树相反）。

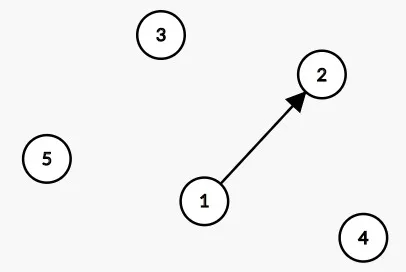
我们首先判断是否构成了环：

查看1所指向的节点, 即b[1] = 2
查看2的父节点, 即a[2] = 2, 因为此时2的父节点就是它自己，所以停止搜索。此刻认定1所指向的节点的根是2
判断1是不是1所指向的节点的根，即1是否等于2
此时不相等，所以没有构成环。没有构成环则更新1的根，即更新a[1]的值为2。

index	1	2	3	4	5
a	2	2	3	4	5
b	2	4	2	3	1

Step 2. 扫描2

当扫描到2时，发现2传递信息给4(即b[2]值为4)，可以用以下的有向图表示。

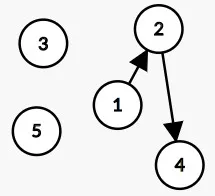
index	1	2	3	4	5
a	2	4	3	4	5
b	2	4	2	3	1

Step 3. 扫描3

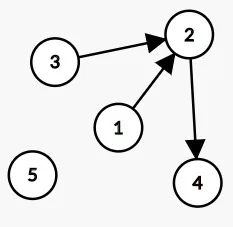
index	1	2	3	4	5
a	2	4	2	4	5
b	2	4	2	3	1

Step 4. 扫描4

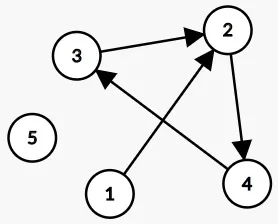
index	1	2	3	4	5
a	2	4	2	4	5
b	2	4	2	3	1

从图上我们可以发现出现了一个环，代码上是如何发现的呢：

查看4所指向的节点, 即b[4] = 3
查看3的父节点, 即a[3] = 2
查看2的父节点, 即a[2] = 4
查看4的父节点, 即a[4] = 4, 因为此时4的父节点就是它自己，所以停止搜索。此刻4所指向的节点的根是4
判断4是不是 4所指向的节点 的根，即4是否等于4
如果相同则认为构成了环。此时构成了环，为了避免循环，则不更新a[4]

Step 5. 扫描5

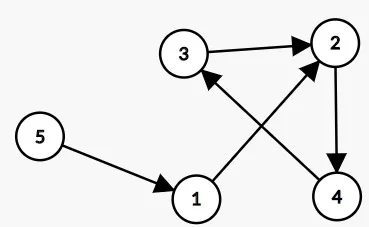
index	1	2	3	4	5
a	2	4	2	4	1
b	2	4	2	3	1

题解 P2661 【信息传递】代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


#include <iostream>
#include <cstdio>
using namespace std;
const int N = 200010;
int n, fa[N], ans = 0x3f3f3f3f;
int get (int x, int &cnt) { //cnt记录环的长度 
    cnt ++;
    if (fa[x] == x) return x;
    else return get(fa[x], cnt);
}
int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++)
        fa[i] = i;
    for (int i = 1; i <= n; i ++) {
        int cnt = 0, f;
        scanf("%d", &f);
        if (get(f, cnt) == i) {
            ans = min(ans, cnt); //维护最小的环 
        }else
            fa[i] = f;
    }
    printf("%d", ans);
    return 0;
}

参考资料

Graph Editor https://csacademy.com/app/graph_editor/ (画图论相关的图片非常好用)
P2661 信息传递题解 https://www.luogu.org/problemnew/solution/P2661 （提供这道题的C代码）

题解 P2661 【信息传递】https://duoluoluo.blog.luogu.org/solution-p2661 （提供这道题的C代码）

目录

并查集

题记