题记
一年半之前写了一篇回溯算法的博客, 不过只是简单的了解了一下,真要写题还是写不出来(过了一年半,不会写的题还是不会写),所以再集中刷一下题.
回溯法通常应用在树形问题上.
入门题
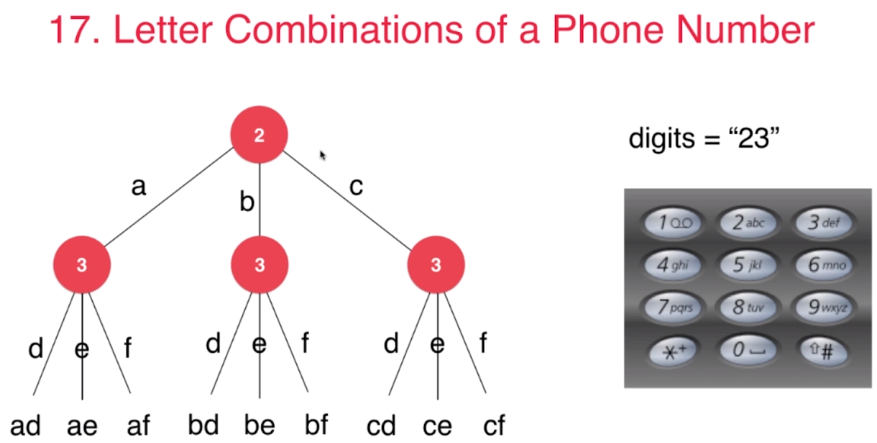
先看一到题,用来复习回溯算法的写法,和所谓树形问题的特点.

s( digits[0…n-1] ) = letter(digits[0]) + s( digits[1…n-1] )
= letter(digits[0]) + letter(digits[1]) + s( digits[2…n-1] )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if digits == "":
return list() # 如果不做这个判断,结果会返回错误答案[""]
phoneMap = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
res = []
def backtrack(index, s):
if index == len(digits):
res.append(s)
return
for d in phoneMap[digits[index]]:
backtrack(index + 1, s + d)
# 如果s用list表示,上面一句的代码应分成下面的三行
# s.append(d)
# backtrack(index + 1, s)
# s.pop()
backtrack(0, "")
return res
|
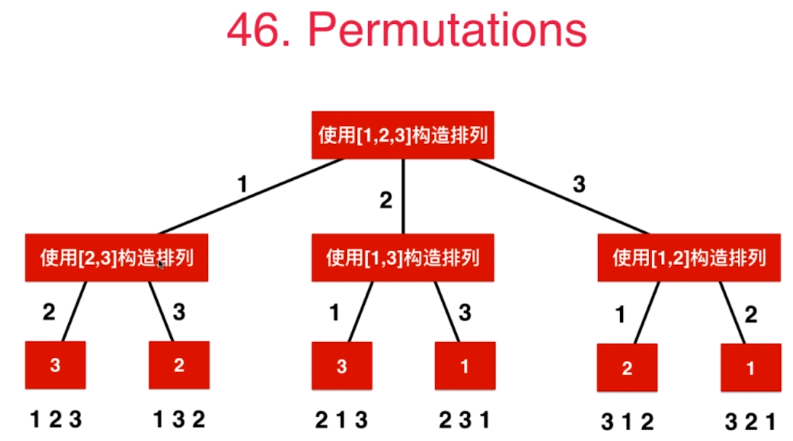
排列问题

Perms(nums[0…n-1]) = {取出一个数字} + Perms(nums[{0…n-1} - 取出的数字]). 与前面的17题的区别是,这里一旦取出了一个数字,后面就不能再取.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
if not nums:
return []
# used = [False] * len(nums)
res = []
def backtrack(index, p):
if index == len(nums):
res.append(p[:]) # 在python中需要复制一次p,否则后续p改变了,会影响res中已经压入的p
return
for i, n in enumerate(nums):
if n in p: # 判断是否这个数字已经使用,也可以通过一个bool的数组实现,从而用空间换时间
continue
#if used[i]:
# continue
p.append(n)
# used[i] = True
backtrack(index+1, p)
p.pop()
# used[i] = False
backtrack(0, [])
return res
|
与上题的区别是,数组会有相同的元素,如输入[1,1,2],输出为[1,1,2],[1,2,1],[2,1,1].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
if not nums:
return []
nums.sort() # 先排序
res = []
used = [False] * len(nums)
def backtrack(index, p):
if index == len(nums):
res.append(p[:])
return
for i, n in enumerate(nums):
if used[i]:
continue
if i > 0 and n == nums[i-1] and not used[i-1]: # not used[i-1]比较难想到
continue
p.append(n)
used[i] = True
backtrack(index+1, p)
p.pop()
used[i] = False
backtrack(0, [])
return res
|
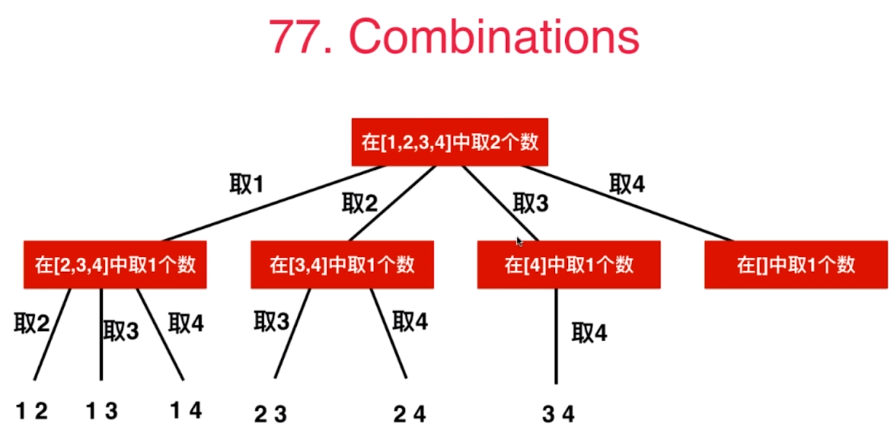
组合问题
输入n=4,k=2; 输出[[1,2], [1,3], [1,4], [2,3], [2,4], [3,4]], 注意[1,2]和[2,1]是一个组合.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if n<=0 or k<=0:
return []
res = []
def backtrack(index, p):
if len(p) == k:
res.append(p[:])
return
for i in range(index, n+1):
p.append(i)
backtrack(i+1, p)
p.pop()
backtrack(1, [])
return res
|
回溯法解决组合问题的优化——剪枝
还是上面的77题,如图示我们发现, 实际上只需要取1,2,3就可以了,因为取4的话剩下的数的数量不够,所以可以跳过4.也就是可以剪枝.
假设我们最终要遍历到索引x的位置, 即i会便利[start,… x] (注意两边都是闭区间, 写到代码range函数时,里面的参数为x+1).
当前我们已经寻找到 len(p) 个数字, 还需要再寻找 k - len(p) 个数, 所以有 x 至少要大于等于 n - (k-len(p)) + 1.
比如, 之前的图示, 还要找2(k-len(p) == 2 - 0)个数, i需要遍历到取3的位置,也就是 4 - 2 + 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if n<=0 or k<=0:
return []
res = []
def backtrack(start, p):
if len(p) == k:
res.append(p[:])
return
for i in range(start, n - (k - len(p)) + 1 + 1): # 剪枝,不需要遍历到i==n的地方
p.append(i)
backtrack(i+1, p)
p.pop()
backtrack(1, [])
return res
|
组合题:
-
- Combination Sum
-
- Combination Sum2
-
- Combination Sum III
-
- Subsets
-
- Subsets II
-
- Binary Watch
二维平面上使用回溯法
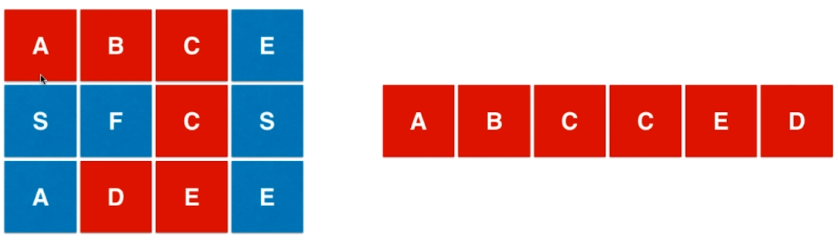
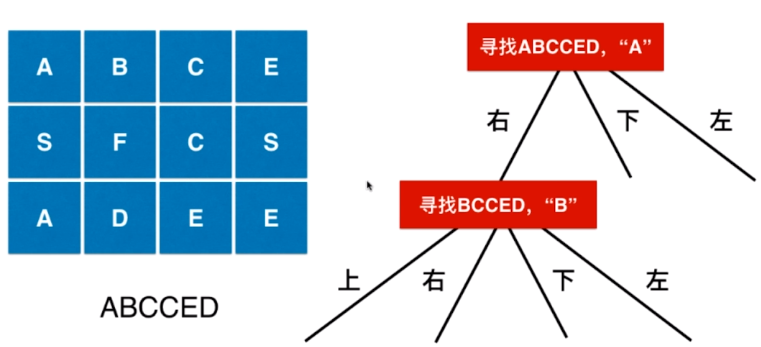
79. Word Search
board =
[
[‘A’,‘B’,‘C’,‘E’],
[‘S’,‘F’,‘C’,‘S’],
[‘A’,‘D’,‘E’,‘E’]
]
给定 word = “ABCCED”, 返回 true
给定 word = “SEE”, 返回 true
给定 word = “ABCB”, 返回 false


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m, n = len(board), len(board[0])
if len(word) == 0:
return True
used = [[False]*n for _ in range(m)]
def searchWord(index, startx, starty):
if index == len(word)-1 and word[index] == board[startx][starty]:
return True
if word[index] == board[startx][starty]:
used[startx][starty] = True
# 四个方向可以用一个数组[[-1,0], [0,1], [1,0], [0,-1]]和一个for循环的方式替换下面的代码
# 是否超过边界,可以定义一个函数inArea(x,y)
# 上
if startx >= 1 and not used[startx-1][starty]:
if searchWord(index+1, startx-1, starty):
return True
# 下
if startx < m - 1 and not used[startx+1][starty]:
if searchWord(index+1, startx+1, starty):
return True
# 左
if starty >= 1 and not used[startx][starty-1]:
if searchWord(index+1, startx, starty-1):
return True
# 右
if starty < n - 1 and not used[startx][starty+1]:
if searchWord(index+1, startx, starty+1):
return True
used[startx][starty] = False
return False
for i in range(m):
for j in range(n):
if searchWord(0, i, j):
return True
return False
|
二维平面中的经典算法——floodfill算法
这个算法的本质就是深度优先遍历.
200. Number of Islands
0代表水,1代表陆地,求陆地组成的岛屿的数量.
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
if n == 0:
return 0
d = [[0,1], [1,0], [-1,0], [0,-1]]
res = 0
visited = [[False] * n for _ in range(m)]
def isArea(x, y):
return x >= 0 and y >=0 and x < m and y < n
# 从grid[x][y]的位置开始进行floodfill
def __dfs(x, y):
visited[x][y] = True # 由于我们需要把和岛屿相连接的所有岛屿标记成True,而没有反过来标记成False的过程,所以有些地方不把这个归为回溯,不过这个方法可以很明确的叫做floodfill
# 向四个方向进行搜索遍历
for i in range(4):
new_x = x + d[i][0]
new_y = y + d[i][1]
# 由于递归保证x,y合法, 且grid[x][y]是没有访问过的陆地,所以实际上递归的终止条件隐含在这里了,终止条件就是走到一个地方四个方向都是非法的
if isArea(new_x, new_y) and not visited[new_x][new_y] and grid[new_x][new_y] == '1':
__dfs(new_x, new_y)
for i in range(m):
for j in range(n):
if not visited[i][j] and grid[i][j] == '1':
res += 1
__dfs(i,j)
return res
|
130 Surrounded Regions

417 Pacific Atlantic Water Flow
找到同时能够流向太平洋和大西洋的地方,如下图括号处的结果.

回溯法是经典人工智能的基础
因为经典(传统)人工智能很多是基于搜索的,所以经常使用回溯.
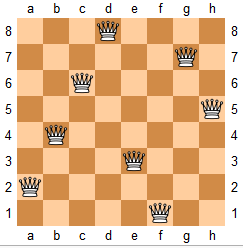
51 N-Queens
n皇后问题研究的是如何将 n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击, 即竖线横线2条斜线4条线不同时出现2个或以上皇后。

输入:4
输出:[
[".Q..", // 解法 1
“…Q”,
“Q…",
“..Q."],
["..Q.", // 解法 2
“Q…",
“…Q”,
“.Q.."]
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
if n <= 0:
return []
res = []
col = [False] * n # 用于判断列是否冲突
dia1 = [False] * (2*n-1)
dia2 = [False] * (2*n-1)
def gernerateBoard(row):
# [1,3,0,2] ->
# [".Q..", // 解法 1
# "...Q",
# "Q...",
# "..Q."]
assert len(row) == n
board = []
for x in row:
tmp = ["."]*n
tmp[x] = 'Q'
board.append(''.join(tmp))
return board
# 尝试在n皇后问题中,摆放第index行的皇后,将摆放结果放在row中
def putQueen(index, row):
if index == n:
res.append(gernerateBoard(row))
return
# 能否将第index行的皇后放在第i列
for i in range(n):
# 如果纵方向和对角线方向都不冲突就可以放
if not col[i] and not dia1[index + i] and not dia2[index-i+n-1]:
row.append(i)
col[i] = True
dia1[index + i] = True
dia2[index-i+n-1] = True
putQueen(index+1, row)
col[i] = False
dia1[index + i] = False
dia2[index-i+n-1] = False
row.pop()
putQueen(0, [])
return res
|
-
52 N-Queens
-
37 Sudoku Solver
参考资料