命题逻辑和自然推演
题记
为了严谨地描述一些问题,我们需要一些语言去表达问题中的逻辑结构,这篇博客将讲述其中一种语言——命题逻辑(propositional logic),
声明式语言(Declarative sentences)
命题逻辑是基于声明式(declarative)语句的,即能够判别真假的语句.
(It is based on propositions, or declarative sentences which one can, in principle, argue as being true or false. )
声明式语句的例子:
- The sum of the numbers 3 and 5 equals 8.
非声明式(non-declarative)语句的例子:
-
Could you please pass me the salt?
-
Ready, steady, go!
相比非声明式, 我们专注于声明式语句,是因为它符合计算机系统/程序的行为,此外,使用声明式语句能够用于判断程序是否满足需求/规格说明(specification).
格式化声明式语言(Formalize declarative sentences)
所谓Formalize, 主要是为了3点:
- 能够有效地进行论证
- 能够严密地定义(defined rigorously)
- 能够被执行
非常自然的formalize的方法就是使用符号(symbol).
Example
-
- 如果公交车晚点, 而且没有出租车, 那么John就会迟到.
- John没有迟到
- 火车晚点了
- 因此, 有出租车
-
- 下雨了, Jane没带伞, 那么Jane就会淋湿
- Jane没有淋湿
- 下雨了
- 因此, ,Jane带伞了
Structures
| Example1 | Example2 |
|---|---|
| 公交车晚点 | 下雨了 |
| 有出租车 | Jane带伞了 |
| John迟到了 | Jane淋湿了 |
Formal argument
其实上面的两个问题属于同一个问题,可以用下面的符号来表示.
If p and not q, then r. -> Not r.p. Therefore, q.
自然推演(Natural deduction)
我们希望建立一套规则(a set of rules)去通过给定的前提(premise)来推出一些结论(conclusion). 其中一个非常重要且普遍的规则称为自然推演.
先了解一些名词和符号:
-
¬ :negation 逻辑否定
-
∧ :conjunction 逻辑合取
-
∨ :disjunction逻辑析取
-
→:implication蕴涵
-
sequent : 一种通过前提证明出结果的意图(intension), 相当于一个证明题的提问部分(区别于证明完成之后的结论)
.
在谈及自然推演规则之前想聊一些别的话题。其实自然推演我们早就在中学或者本科的离散数学里学习过,中学课程会告诉我们这是很正常的思想(比如否定的否定就是不变,¬¬p可以变成p),本科会通过真值表定义这些规则. 但是逻辑学想说的是,这些符号规则本身没有意义, 也就是说我们完全可以定义一套规则说¬p可以变成p, 而我们之所以默认使用自然推演这套规则,仅仅是因为他能解决实际生活中的很多问题(比如之前John迟到的例子). 很多数学家一生所做的事情就是自己根据自己制定的规则,然后不断推导,得到一些性质,这些规则本身其实毫无意义,只不过如果幸运的话这套规则可能能够运用到一些场景中,想到一句话——数学不是科学,因为数学不能被证伪.
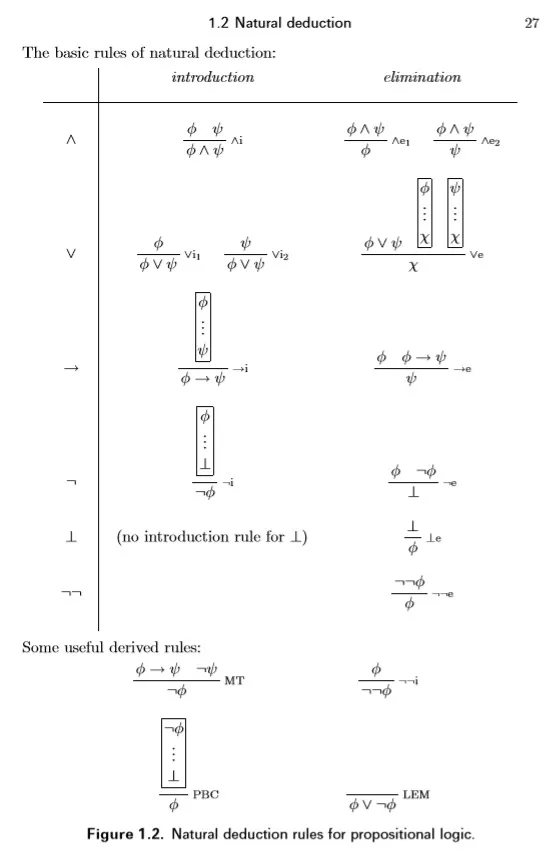
现在给出自然推演的一些规则,需要说明的下面使用的表达方法可能以前少见,但是它是在顶刊中大家公认的表达方式,即
$$ \frac{premise \ premise}{conclusion} rule $$ 其中上面的"rule"只是指规则的名字,比如某个规则名为"$\wedge i$”. 推演规则分类为introduction(用于定义符号)和elimination(用于消去符号,以达到推演的目的).
Rules for conjunction
- And-introduction rule
$$\frac{\phi \qquad \psi}{\phi \wedge \psi} \wedge i$$
- And-elimination rules
$$ \frac{\phi \wedge \psi}{\phi} \wedge e_{1} $$
$$ \frac{\phi \wedge \psi}{\psi} \wedge e_{2} $$
Rules of double negation
- Introduction rule $$ \frac{\phi}{\neg \neg \phi} \neg \neg i $$
- Elimination rules $$ \frac{\neg \neg \phi}{\phi} \neg \neg e $$
现在我们用上面的规则就可以解下面这道题目了(第三行"$\neg \neg i \ 1$"的意思是根据规则"$\neg \neg i$"和第一行的p,后面同理).

Rules of implication
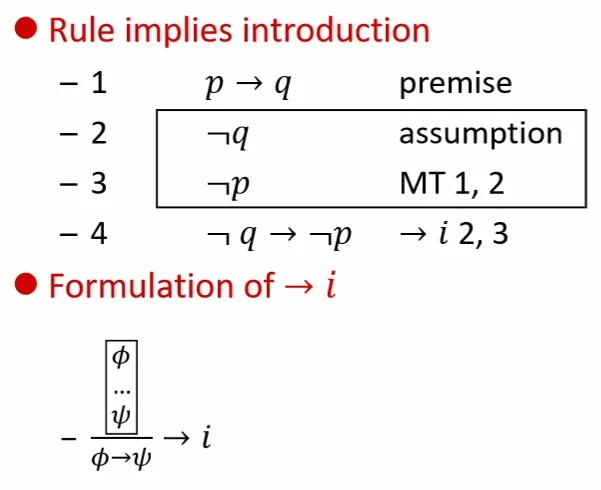
- Introduction
这里使用到假设的方法,用方框框住的区域为假设区域,假设的内容只在方框内有效, 方框内可以使用方框外的信息.

- Implies-elimination rule $$ \frac{\phi \quad \phi \rightarrow \psi}{\psi} \rightarrow e $$
- Modus Tollens (MT for short) rule 即 逆否命题,可以通过其他规则(primitive rule)推导得出的规则(称为derived rule) $$ \frac{\phi \rightarrow \psi\quad \neg \psi}{\neg \phi} \mathrm{MT} $$
Rules of disjunction

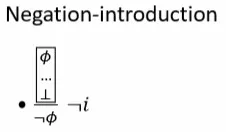
Rules of negation
为了定义否命题(注意前面只是定义了double negation),需要引入contradiction(矛盾)来完备自然推演这套规则. 定义contradiction: Contradictions are expressions of the form $\neg \phi \wedge \phi$ or $\phi \wedge \neg \phi$, where $\phi$ is an arbitrary formula.
(Note that $p \wedge \neg p \vdash q$ is valid. 可以理解成如果你连矛盾的事情都能推出来, 还有什么推不出来呢,。但是注意这样只是便于理解,要记住符号本身没有任何意义.)
- Bottom-elimination 即 $$ \frac{\perp}{\phi} \perp \mathrm{e} $$
- Not-elimination $$ \frac{\phi \quad \neg \phi}{\perp} \neg e $$
例题

总结